N-Body Simulation

Source

Per course policy, access to code is only granted upon request.

Result Showcase

The Problem

In this project, we aim to provide an efficient method to simulate the N-Body problem widely explored in physics and astronomy. The N-Body simulation is defined by Wikipedia as follows:

An N-body simulation is a simulation of a dynamical system of particles, usually under the influence of physical forces, such as gravity.

We plan to model the movement of a vast number of particles with initial positions, speed, and mass. We mainly model two phenomena: (a) the effect of gravity among particles, and (b) the effect of collision between two particles.

Gravity

We assume that gravity exists between any two particles with mass. We calculate gravity based on the formula given by Newton:

where \(G\) is the gravitational constant, \(m_1,m_2\) are the mass of the two objects experiencing gravitational force, and \(r\) is the distance between the pair.

Based on the gravity between a pair of particles, we can calculate the acceleration exerted by this force on the two particles, and thus the speed of the particles in the next iteration.

Collision

As particles fly through space, there is a chance that two particles may hit each other head-on. We assume that each particle has no volume, so every collision will always be head-on. We also assume that the collision is completely elastic, so no kinetic energy is lost in this process. With these two assumptions, we can calculate the speed after the collision through preservation of momentum and kinetic energy. We can use the following formula to calculate speed of the objects after collision:

where \(\textbf{v}_1,\textbf{v}_2\) are the initial speed vectors of the two particles, \(\textbf{v}_1',\textbf{v}_2'\) are the resulting speed vectors after the collision, and \(\textbf{x}_1,\textbf{x}_2\) are the position vectors.

The Naive Approach

The naive approach for gravity calculation and collision detection will take \(O(n^2)\) time each, where \(n\) is the number of particles in the simulation box.

• To calculate the gravity force exerted on each particle, we will need to calculate the gravity exerted by the other \(n-1\) particles. Thus, calculating the gravity force for each particle takes \(O(n)\) time, and the calculation for the whole system takes \(O(n^2)\) time.
• To check whether one particle has collided with another particle, we will need to calculate the distance between the particles, and if the distance is closer than some predefined cutoff value, we treat the two particles as if they have collided. We need to check whether collision happen between any two pairs of particles, and since there are \(O(n^2)\) pairs, checking would also take \(O(n^2)\) time.

Since we want to simulate the movement of a huge number of particles, we would want our algorithm for simulation to be as efficient as possible. We try to push the efficiency beyond \(O(n^2)\) through taking advantage of the data structure called quad tree.

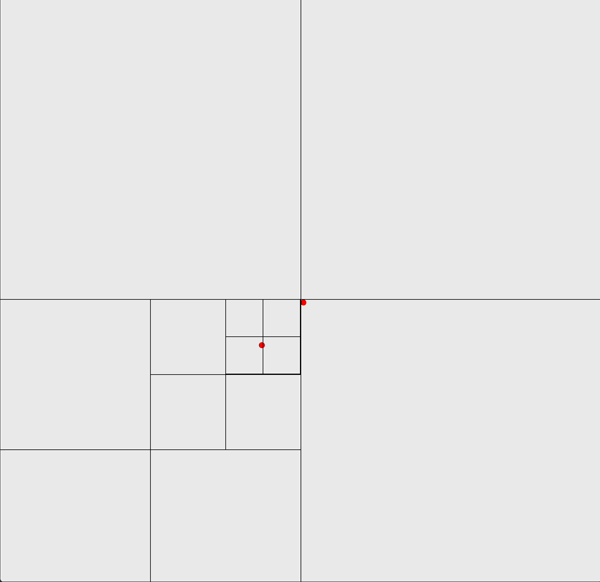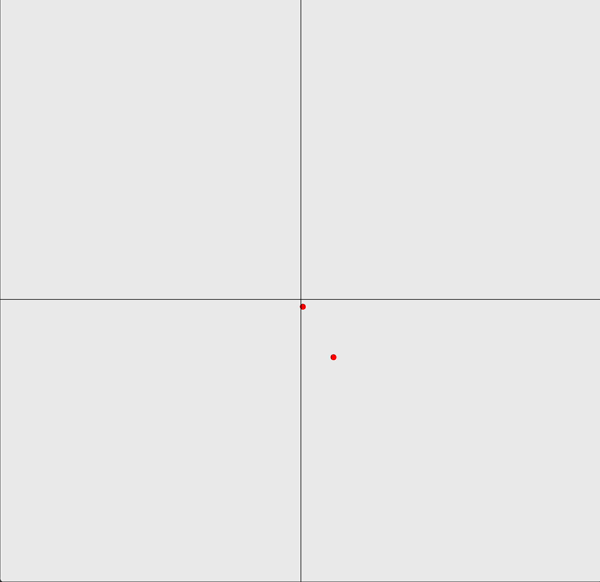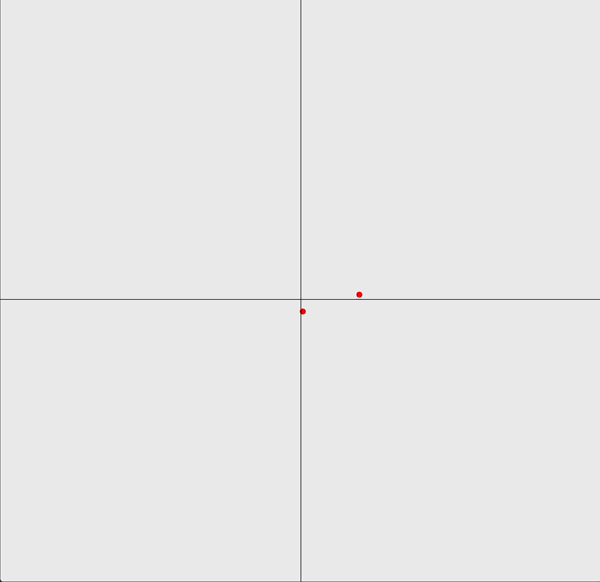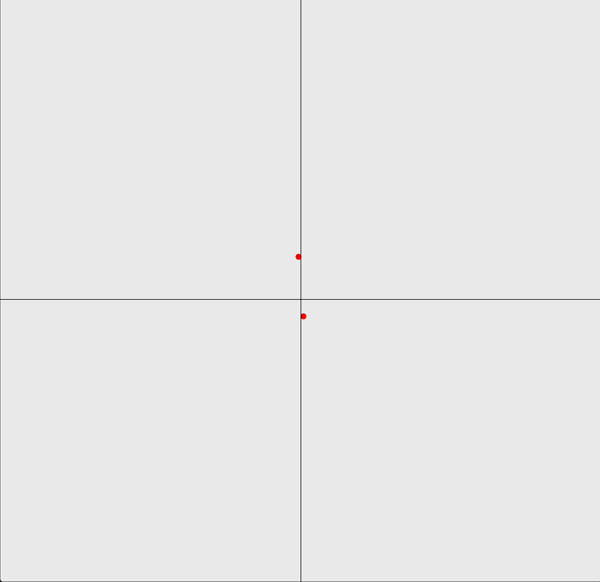
Our Implementation through Quad Tree

We choose to use a quad tree to speed up our calculation for gravity and collision detection. This improves the run time of our algorithm to \(O(n \log n)\). A quad tree is a recursive data structure used to store spatial information. Each node in the quad tree represents a quadrant of a given region, and the four children of the node represent the sub-quadrants if we divide up the quadrant along the vertical and horizontal axes.

Approximating Gravity

This data structure can help us approximate the gravity force very efficiently. We approximate the gravity force exerted on a given particle by merging particles that are far away from our given particle to a single particle, called centroid, residing at the center of mass of the particles. Through this approximation, we no longer need to do pairwise calculation between particles that are far away from each other. Instead, we calculate the force exerted on one particle from a cluster of particles together.

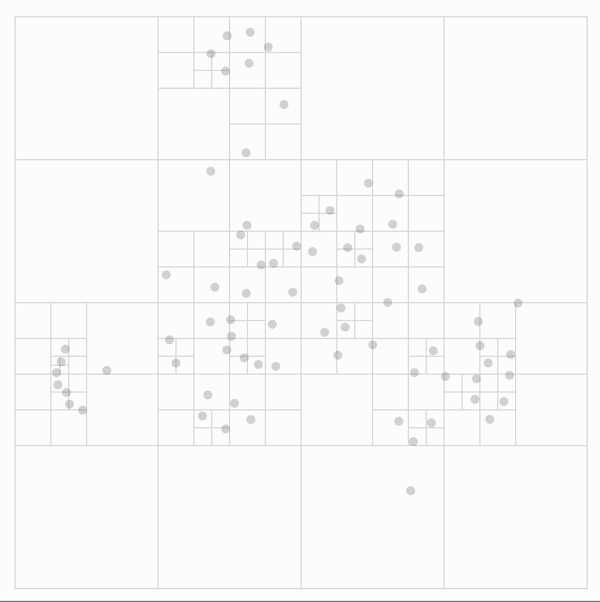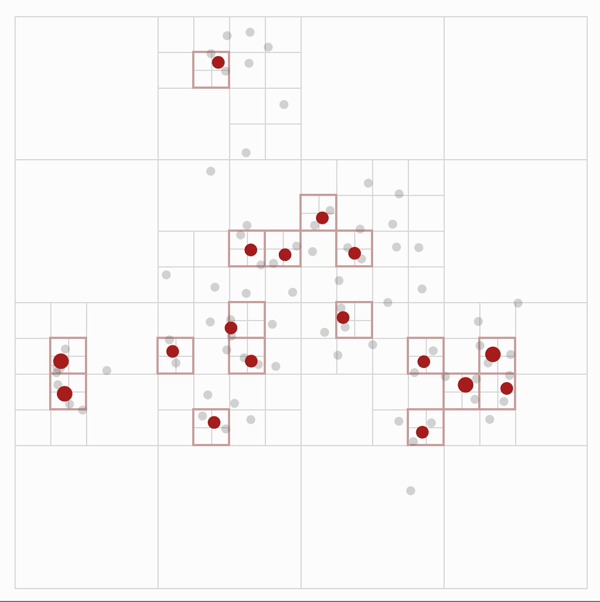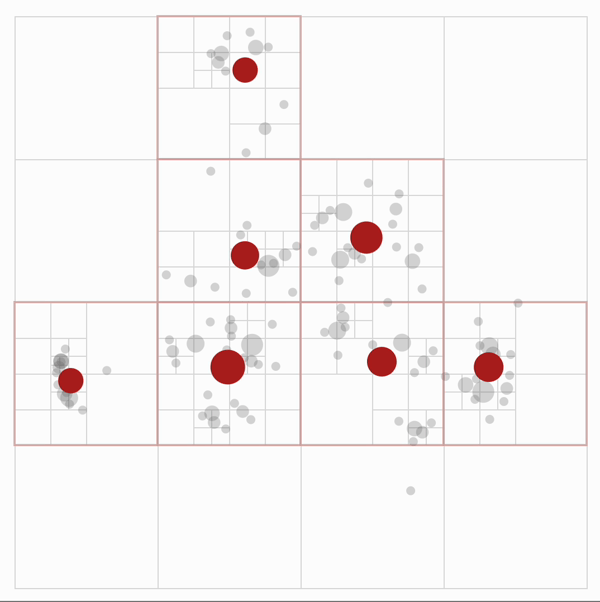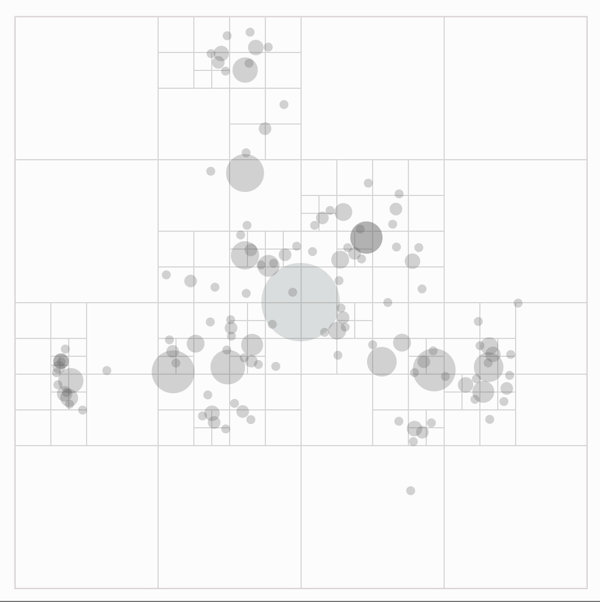
Credit: The Barnes-Hut Approximation

The specific implementation for this method is to recursively build up centroids at each level when we traverse the quad tree in post-order. But one thing that we should note is that this approximation does not work when the particles are too close to each other. Therefore, we define a parameter \(\theta\) to be the cutoff point, and if the ratio of the length of the side of the quadrant to the distance between the two particles is greater than this value, i.e. the two particles are too close, we will use pairwise calculation instead of this approximation. Because the maximum depth we will reach is the height of the quad tree, this method yields \(O(\log n)\) time for calculating the gravity for each particle, and cumulatively \(O(n \log n)\) time.

Detecting Collision

To detect collision, we first define a collision distance, and if the distance between two particles is less than the collision distance, we consider that the particles have collided. Next, we define the minimum length of the quadrant in the quad tree to be at least the length of the collision distance. In this way, we will also have a maximum height of the quad tree.

In our implementation, two particles have collided if they share the same quadrant and that quadrant can no longer be subdivided (i.e. we have reached the maximum height). Then it is easy to check if a particle is involved in some collision: we simply find the particle in the quad tree, and check, first, if the quadrant the particle is in a minimum quadrant, and second, if any other particle also exists in the quadrant. This only takes \(O(\log n)\) time because the search path in the quad tree is at most the height of the tree.

In the edge case where multiple particles exist in the same minimum quadrant, we treat the collision sequentially. In the case where there are three particles, the two particles that are closest collide first, then the particle that is closest to the third collides with the third.