CUDA Flocking Simulation
A CUDA-based flocking simulation, written in C++.
Tested on: Windows 11, i5-11600K @ 3.91GHz 32GB, RTX 2060 6GB (Personal Desktop)
Visualizations
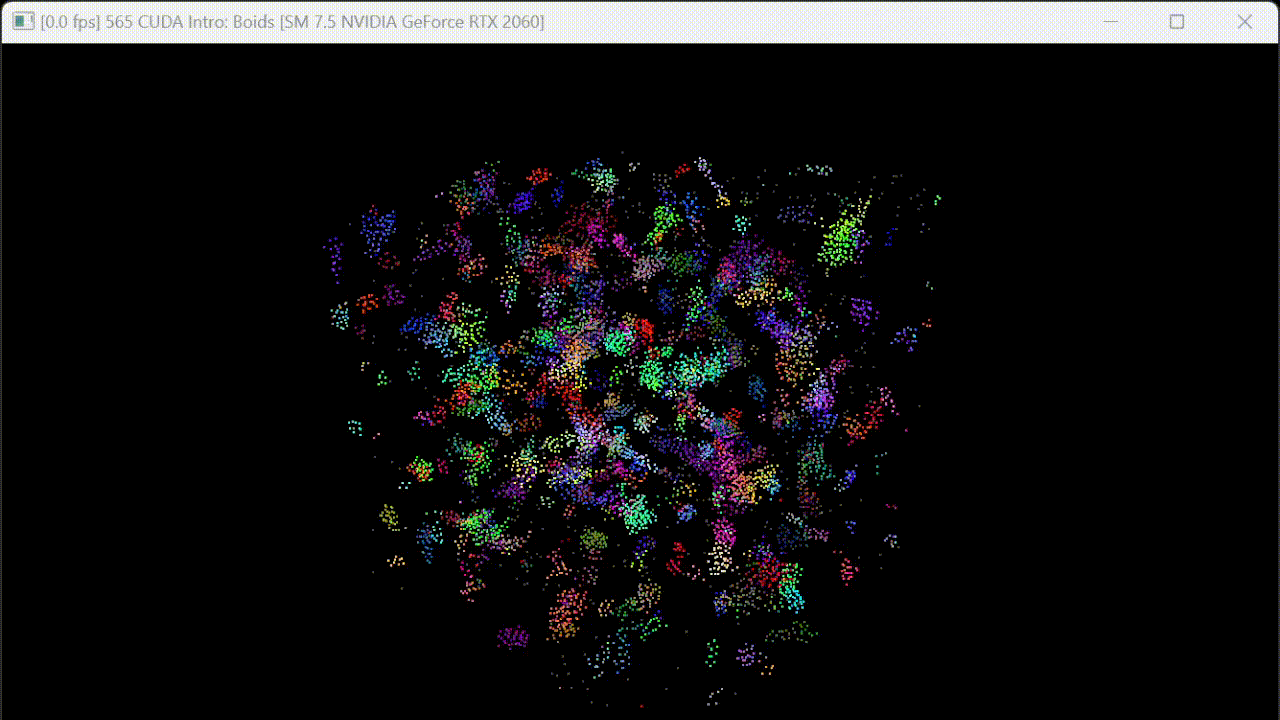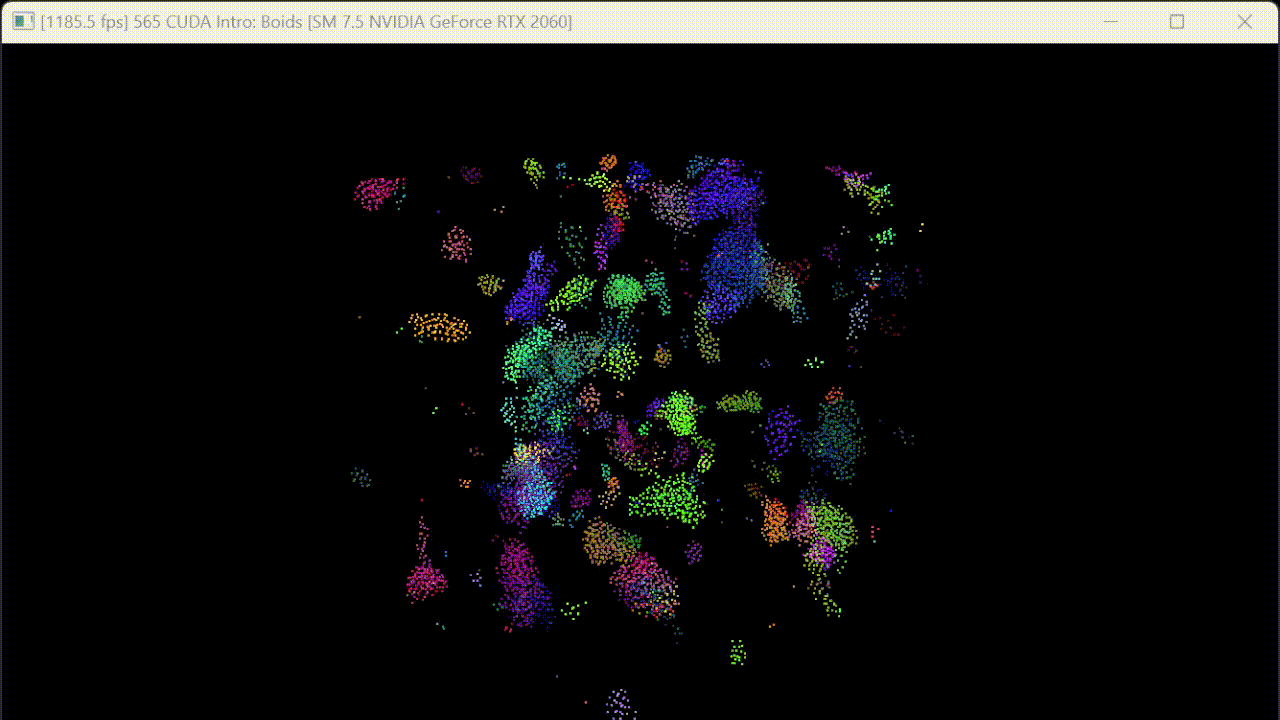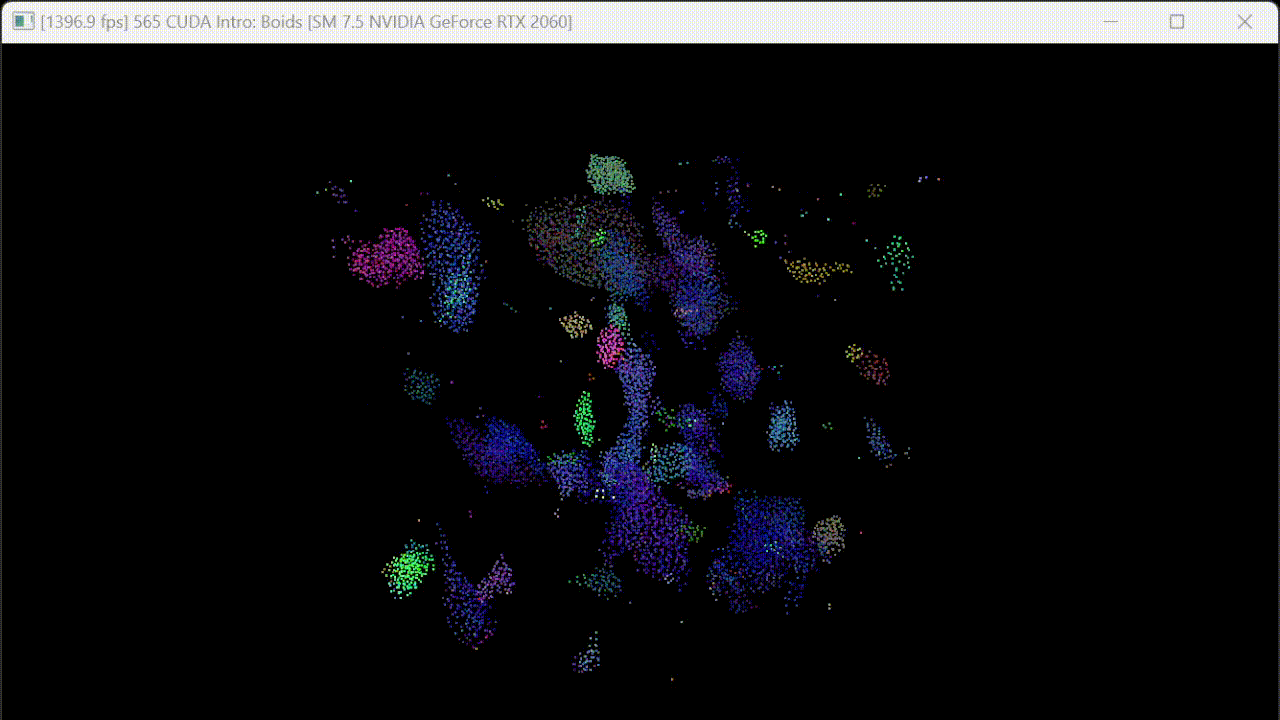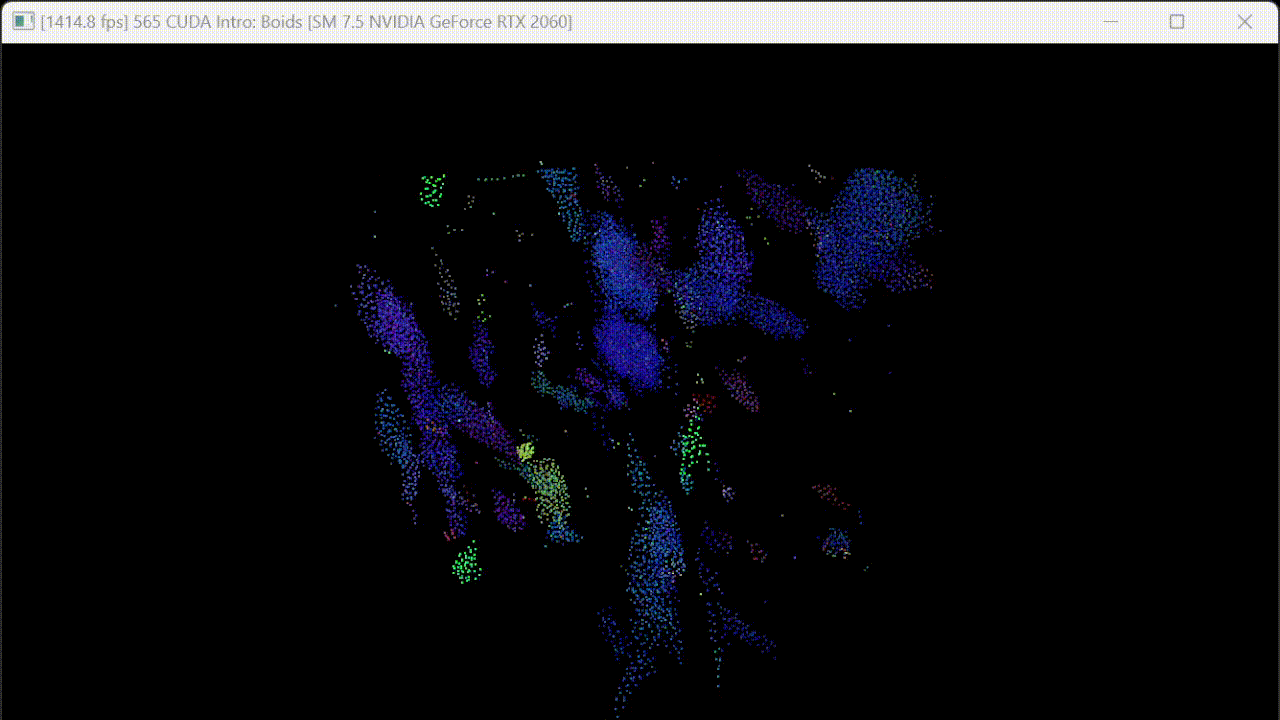
Performance Analysis
To measure the performance of the simulation accurately, FPS info is measured at each configuration with visualization disabled.
1. FPS vs. #Boid
With every other parameter fixed, I tested FPS at the following #boid: 1000 5000 10000 50000 100000 200000 500000.

FPS vs. #Boids
Block Size = 128, Scene Scale = 100.0
We can see that all implementations has decreasing FPS when #boid increases. This is likely due to drastically more compute loads due to more boids and more neighbors to consider. The naive implementation has the fastest FPS decrease while the coherent implementation has the slowest decrease, which is due to uniform grid optimization and faster data fetching by rearranging data buffers.
It is worth noting that when #boid is very small, at around 1000, the naive implementation is actually faster than the simple uniform grid implementation. This might be due to very limited number of neighbors to consider, which leads the optimization overheads to standout.
2. FPS vs. Block Size
Block size at 1 5 10 20 50 100 200 500 are tested to measure the FPS performance.

FPS vs. Block Size
Scene Scale = 100.0 #Boid = 10k
We can see that FPS increases with block size for all implementations and generally stops increasing as block size is over 32. This is becuase the maximum number of concurrent wraps per SM on Turing GPUs (RTX 2060) is 32. When launching kernels with block that has size smaller than 32, each wrap will be underutilized, leading to idle core and resource waste.
Questions:
- For each implementation, how does changing the number of boids affect performance? Why do you think this is?
In all three implementations, increasing #boids decreases the performance. This is because new velocity and new position must be calculated for each boid, and there is a hardware limit of how much calculation for each boid can be parallelized. When passed, increasing #boids will require more time as we cannot parallelize calculations for all boids. Besides, when holding other parameters, increasing #boids requires to check more neighboring boids to update its velocity, which leads to more time cost and lower performance.
- For each implementation, how does changing the block count and block size affect performance? Why do you think this is?
As analyzed above, increasing the block size leads to increased FPS until a certain point - in my case is 32, beyond which increasing block size has little impact on FPS. This is most likely due to underutilization of wraps because on Turing GPUs, the maximum number of concurrent wraps per SM is 32. When launching a kernel with blocks that have less than 32 threads, some cores will be idle, which leads to waste of resources.
- For the coherent uniform grid: did you experience any performance improvements with the more coherent uniform grid? Was this the outcome you expected? Why or why not?
Compared with the original uniform grid implementation, the coherent grid implementation uses rearranged position and velocity data buffers. This means data for boids that are within a cell are gathered more closely together, which means more locality, and thus better utilization of cache and data fetching.
- Did changing cell width and checking 27 vs 8 neighboring cells affect performance? Why or why not? Be careful: it is insufficient (and possibly incorrect) to say that 27-cell is slower simply because there are more cells to check!
From a theoretical perspective, I would predict that checking 27 neighboring cells is actually more efficient than checking 8 cells. Say the maximum radius of all three rules is \(r\). To ensure the surrounding 8 cells contain all potential boids, the side length of each cell must be at least \(2r\). Therefore, the entire volume of space we will check for neighboring boids is \(8(2r)^3 = 64r^3\). Similarly, if we want to check 27 neighboring cells, the size length of each cell must be at least \(r\). Hence the volume of space we will check is now \(27r^3\). We see that this volume is generally smaller than \(64r^3\) - which means we need to check a smaller volume for neighbors. This in turn means a higher hit rate for boids that are actually taken into consideration and in general less boids we have to check. Therefore, checking 27 neighboring cells might be more efficient, if the optimum side length is chosen for cells.